Math Task Framework:
Contributors:
Stephanie Casper
Marissa Minnick
Samantha Townsend
April Warren
A professional development guide.
High Cognitive Demand:
Tasks that require non-algorithmic thinking. Going beyond simply using procedures correctly, high cognitive tasks demand that students investigate the ideas and concepts underlying procedures and their applications to problems.
To identify high cognitive demand tasks, use the categorization criteria included in the table below from Stein, Smith, Henningsen, and Silver (2000) and then read our definitions below.

Note that high cognitive tasks are grouped into two subcategories: procedure with connection and doing mathematics. After familiarizing yourself with the categories and their criterion, read below for examples of high cognitive demand tasks.
High Cognitive Demand Tasks
Procedures with Connections – The task / solution
- Focuses students’ attention on the use of procedures for the purpose of developing deeper understanding of mathematical concepts and ideas.
- Suggests explicit and/or implicit pathways to follow that involve the use of broad general procedures that have close connections to underlying conceptual ideas as opposed to narrow algorithms.
-Can usually be represented in multiple ways, including the use of manipulative materials, diagrams, and symbols. Making connections among the representations helps students develop meaning.
-Requires some degree of cognitive effort. Although general procedures may be followed, they cannot be followed mindlessly. Students are engaged in conceptual ideas that underlie the procedure and develop understanding.
Doing Mathematics – The task / solution
- Requires complex, non-algorithmic thinking.
- Requires students to explore and understand the nature of mathematical concepts, processes, or relationships.
- Demands students do some type of self-monitoring or self-regulation of their own cognitive processes.
- Requires students to access relevant knowledge and experiences and make appropriate uses of them in working through the task
- Requires students to analyze task constraints that may limit possible solution strategies or solutions.
- Requires considerable cognitive effort and may cause some level of anxiety for the students as they are working through the problem.
Definitions
-Procedure with Connection: Procedure with connection tasks suggest the use of a procedure, yet the procedure is better integrated into the problem and students are required to think about the way they apply the procedure to the problem's context. Often, there are multiple ways to solve procedure with connection tasks.
-Doing Mathematics: The highest category of cognitive demand, doing mathematics is best viewed as an investigation of mathematical concepts. With doing mathematics tasks, students must fully understand the mathematical processes in use and enact critical thinking skills.
High Cognitive Task Examples
Answers are provided in orange.
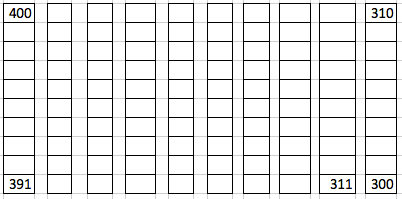
I) Procedure with Connection: Ask students to fill in the blanks in problems A - D below counting backwards by fives. Students may use the charts to the right for help.
A: 400, 395, 390, 385
B: 315, 310, 305, 300
C: 351, 346, 341, 336
D: 392, 387, 382, 377
II ) Doing Mathematics: Have students read Adam and Carlos' solutions and then answer the following questions.
Adam solved 123 - 16 using an empty number line and got the answer 107. Carlos also solved 123 - 16 using an empty number line and also got 107, but tried a different approach than Adam.
- What may have Adam wrote on his number line? What may have Carlos wrote on his number line?
Adam may have written
(123 - 10) (113 - 3) (110 - 3)
123 ------------------- 113 --------------- 110 ----------- 107
Carlos may have written
(126 - 16)
(123 + 3) (110 -3)
126 ---------- 123 --------- 110 --------- 107
- Explain Adam and Carlos' answers and state whether or not each of them are correct.
Both solutions are correct. Adam first subtracted 10 from 123 to get 113, then subtracted 3 to get 110 and subtracted another 3 to get 107. If you add the numbers Adam subtracted, you can tell that he subtracted 16 total, but that he simply did it in
smaller steps. Carlos first added 3 to 123 to get 126, which may have been an easier number from which to subtract 16. After
subtracting 16 from 126 and getting 110, Carlos then has to subtract 3 since earlier he added 3 into the problem. When he
subtracts 3 from 110 he gets 107, which is also correct.